| Métrica | Valor |
|---|---|
| Ratio de Sharpe Actual | 2.3640 |
| Sharpe Máximo Alcanzado | 10.2272 |
| Posición Actual | 94 |
| Mejor Posición Alcanzada | 23 |
| Días en Competición | 220 |
Concurso CFA Society Spain 2025
Optimización de Cartera con Modelos DCC-GARCH: Alcanzando un Sharpe de 2.364
Enlaces del Proyecto
Código completo, datos y metodología
ironia.tech - CFA Society Spain 2025
Resumen del Proyecto
La mejor manera de aprender a invertir no es arriesgando tu propio dinero desde el principio, sino practicando en un entorno controlado donde puedes experimentar, equivocarte y mejorar sin consecuencias económicas reales.
Este proyecto documenta mi participación en el Concurso de Simulación de Gestión de Carteras de CFA Society Spain 2025, donde he aplicado técnicas cuantitativas avanzadas para construir una cartera optimizada que ha alcanzado un Ratio de Sharpe de 2.364.
Características del Concurso
- Organizador: CFA Society Spain 2025
- Plataforma: ironia.tech (broker de simulación)
- Tipo de Competición: Un ganador
- Inscripción: Gratuita (0,00 €)
- Métrica de Evaluación: Ratio de Sharpe
- Mi Estrategia: MMK - DCC-GARCH
¿Por qué Participar en Concursos de Gestión de Carteras?
Los concursos de gestión de carteras son el mejor campo de entrenamiento para aprender inversión porque:
- Puedes probar estrategias sin arriesgar dinero real
- Aprendes a diversificar y gestionar riesgo
- Entiendes cómo funciona el mercado en tiempo real
- La competición te motiva a mejorar constantemente
- Aprendes de las decisiones de otros participantes
- Puedes equivocarte sin consecuencias graves
Metodología: Optimización Cuantitativa con DCC-GARCH
Para construir mi cartera no me he basado en intuición o tendencias del momento, sino en un enfoque cuantitativo riguroso que combina teoría moderna de carteras con econometría avanzada.
Pipeline de Optimización en 7 Pasos
1. Carga y Limpieza de Datos
- Recopilación de precios históricos diarios de Yahoo Finance
- Universo inicial de múltiples fondos de inversión
- Filtros de calidad: datos actualizados y mínimo 5 años de historial (≥1250 observaciones)
- Resultado: 33 símbolos preseleccionados inicialmente
2. Cálculo de Métricas de Riesgo-Retorno
Análisis exhaustivo de cada activo calculando:
- Rentabilidades logarítmicas diarias
- Rentabilidad anualizada y Volatilidad anualizada
- Ratio de Sharpe histórico y Ratio de Sortino
- Máximo Drawdown (caída máxima desde picos)
- Asimetría (Skewness) y Curtosis (colas de distribución)
- Métricas móviles (rolling windows de 21 y 126 días)
3. Preselección de Activos
Reducción del universo aplicando criterios cuantitativos:
- Ranking por Ratio de Sharpe histórico dentro de cada categoría
- Máximo de símbolos por tipo de activo
- Umbrales mínimos de rentabilidad y máximos de volatilidad
- Asegurar presencia de tipos obligatorios (RV, RF, etc.)
- Análisis de correlaciones para detectar redundancias
- Resultado final: 11 activos seleccionados
4. Modelado DCC-GARCH Multivariante
Esta es la parte más avanzada de la metodología. Implementé un modelo DCC-GARCH(1,1) multivariante que:
- Captura la volatilidad cambiante a lo largo del tiempo (heteroscedasticidad)
- Modela correlaciones dinámicas entre activos que varían según condiciones de mercado
- Genera proyecciones de matriz de covarianzas para los próximos 6 meses (126 días hábiles)
- Utiliza distribución MVT (Multivariante t-Student) para capturar colas pesadas
¿Por qué DCC-GARCH?
Los modelos tradicionales asumen volatilidades y correlaciones constantes, lo cual es irreal en mercados financieros. DCC-GARCH permite:
- Adaptarse a cambios de régimen de mercado (tranquilo vs. turbulento)
- Capturar clustering de volatilidad (periodos de alta/baja volatilidad)
- Reflejar que las correlaciones aumentan en crisis (diversificación falla justo cuando más se necesita)
5. Estimación de Retornos Esperados
Para los retornos esperados utilicé medias históricas anualizadas, ya que:
- Los modelos GARCH mejoran volatilidades, pero no retornos medios
- Es un estimador prudente y conservador
- Evita sobre-optimismo basado en tendencias recientes
6. Optimización de Cartera Tangente
Con los inputs proyectados (\(\mu\) y \(\Sigma\)), calculé la Cartera Tangente que maximiza el Ratio de Sharpe:
\[ \text{Maximizar: } \frac{w^T \mu}{\sqrt{w^T \Sigma w}} \]
Sujeto a restricciones:
- Inversión completa: \(\sum w_i = 1\)
- Solo posiciones largas: \(w_i \geq 0\) (sin ventas en corto)
Utilicé el optimizador global DEoptim (Differential Evolution) por su robustez frente a mínimos locales.
7. Selección Final y Análisis de Escenarios
- Reducción a los 6 activos con mayor peso óptimo
- Renormalización de pesos
- Simulación Monte Carlo (100 trayectorias × 3 escenarios × 5 años)
- Evaluación de rendimiento bajo escenarios base, malo y bueno
- Backtesting histórico con pesos fijos
Resultados
Rendimiento de la Cartera
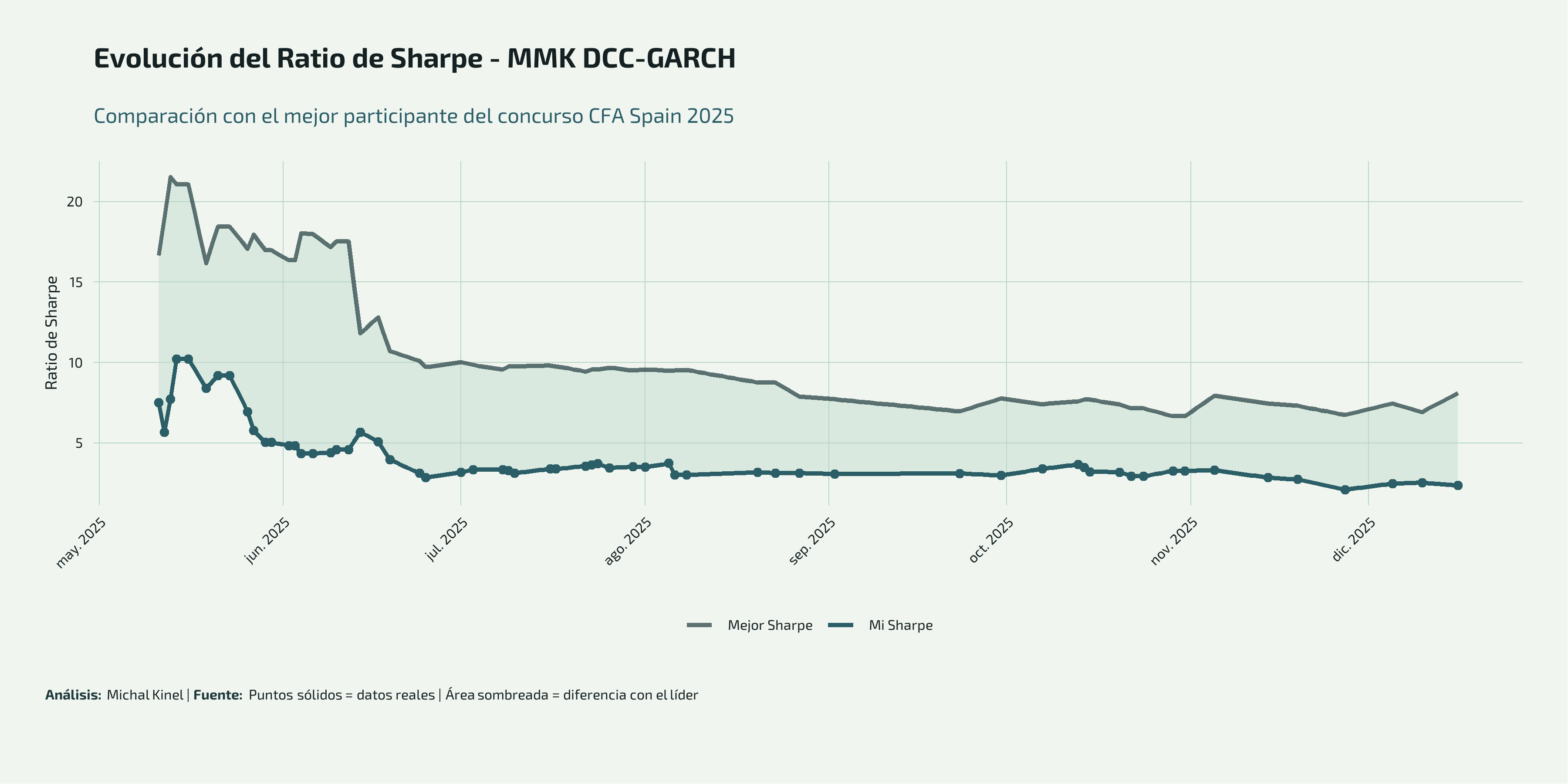
Evolución de las Estadísticas
Durante los más de 7 meses de competición (mayo a diciembre 2025), la estrategia ha mostrado una evolución interesante:
Observaciones clave sobre la evolución del Sharpe:
- Inicio volátil (Mayo): El Sharpe inicial comenzó bajo (~5-7) pero rápidamente escaló a máximos históricos de 10.23 a mediados de mayo, alcanzando la posición 23.
- Consolidación (Junio-Agosto): Después del pico inicial, el Sharpe se estabilizó en el rango 3-5, mostrando menor volatilidad.
- Estabilidad reciente (Septiembre-Diciembre): El ratio se ha mantenido consistente alrededor de 2.5-3.5, demostrando robustez de la estrategia.
El área sombreada muestra el gap con el líder del concurso, que se ha mantenido relativamente constante en términos relativos.
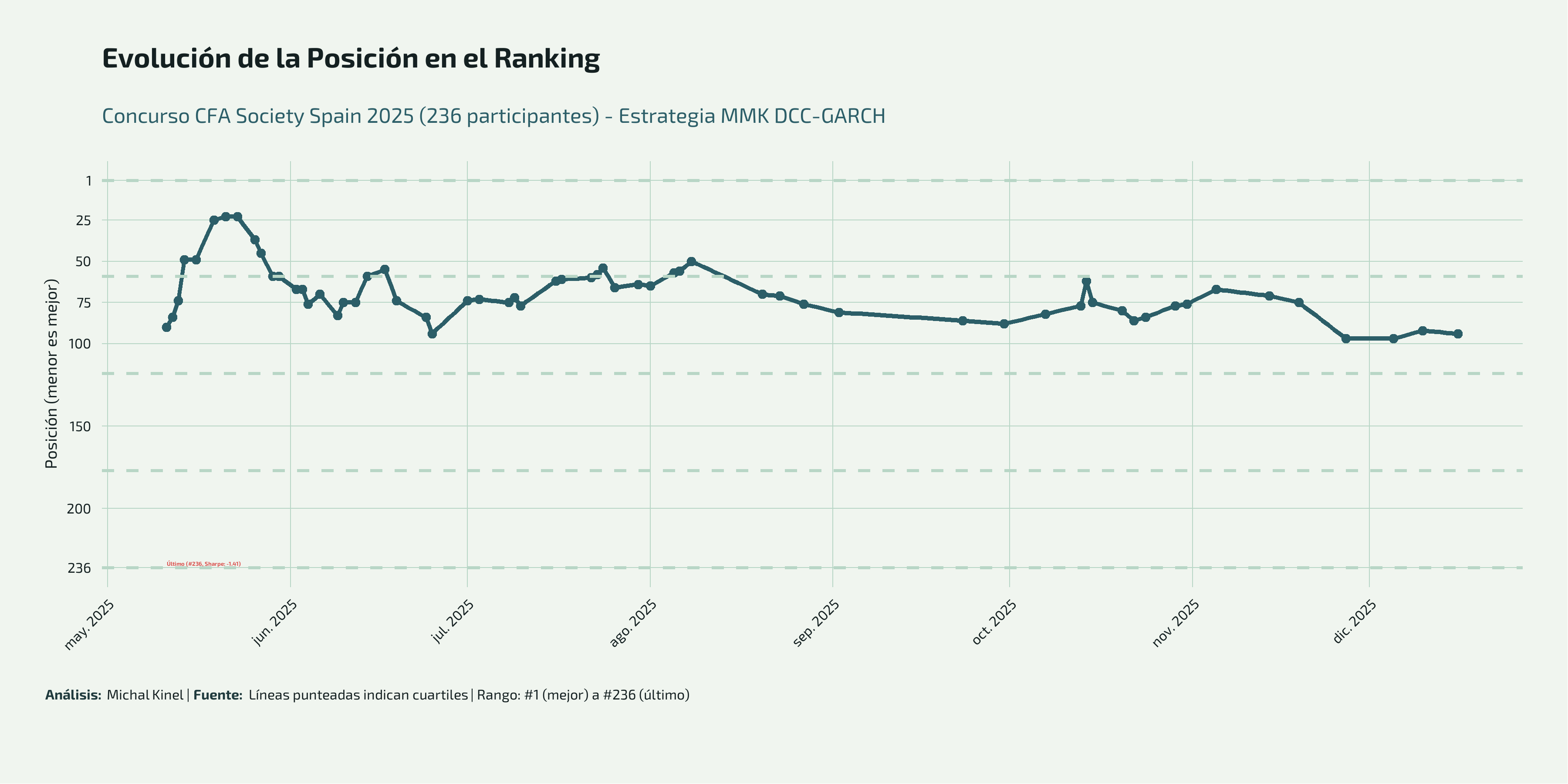
La posición en el ranking ha mostrado variabilidad típica de competiciones de gestión de carteras:
- Mejor momento: Posición #23 de 236 alcanzada en mayo (top 10%)
- Tendencia general: La posición se ha mantenido mayormente en el rango 50-100 (segundo y tercer cuartil)
- Posición actual: #94 de 236 participantes (percentil ~60%)
- Contexto: El último participante (#236) tiene un Sharpe de -1.41, destacando la dificultad del concurso
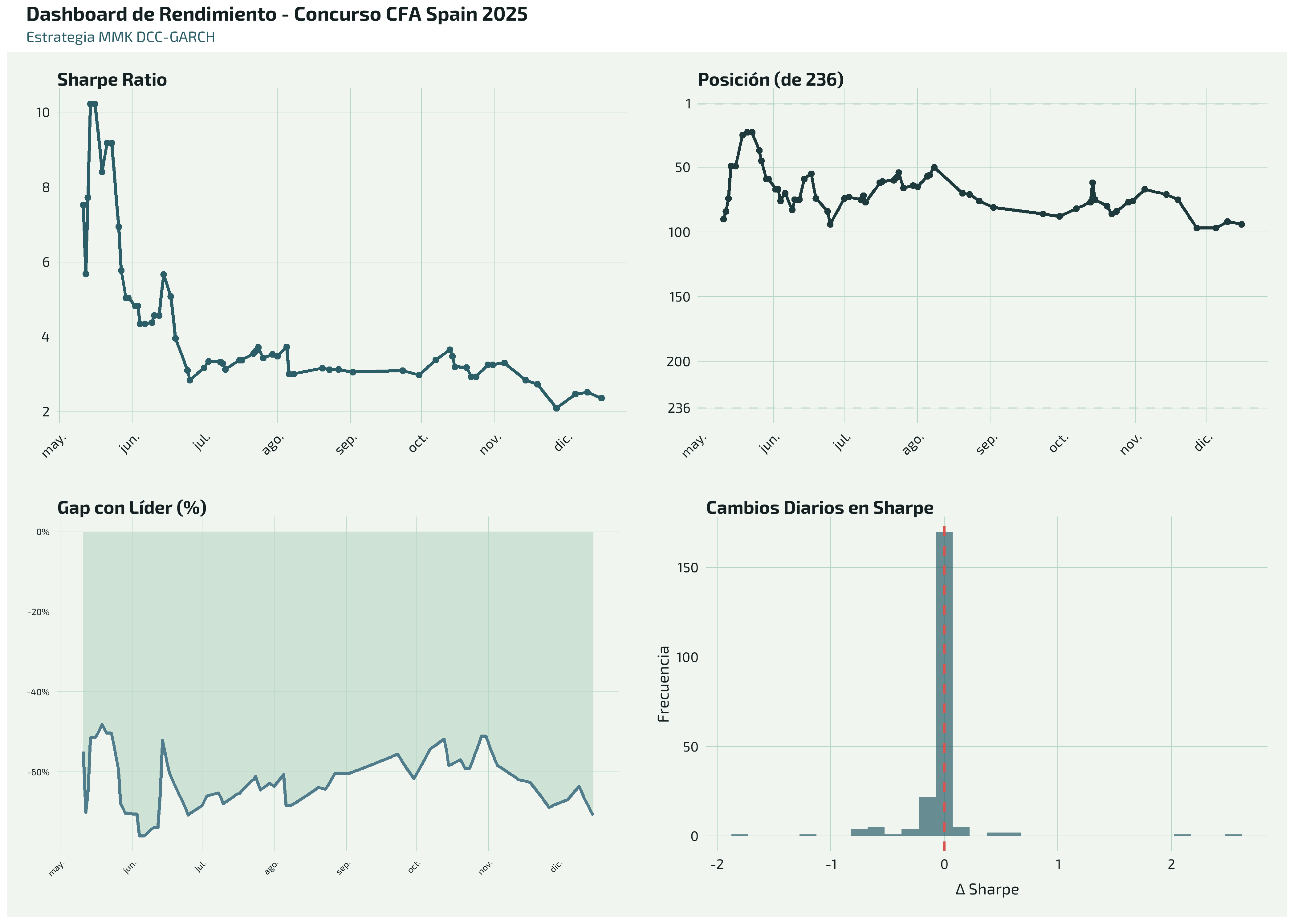
El dashboard combinado muestra:
- Sharpe Ratio (superior izquierda): Tendencia general desde máximos iniciales, pero estable en niveles competitivos
- Posición (superior derecha): Fluctuaciones típicas de competición, con mejora reciente hacia posiciones medias-bajas
- Gap con Líder (inferior izquierda): Se ha mantenido entre 50-70% en términos relativos durante la mayor parte del concurso
- Cambios Diarios (inferior derecha): Distribución concentrada cerca de cero, indicando estabilidad día a día
Un Ratio de Sharpe de 2.364 es un resultado excepcional que indica:
- Alta rentabilidad ajustada por riesgo: Por cada unidad de volatilidad, se obtienen 2.364 unidades de exceso de retorno
- Gestión eficiente del riesgo: La cartera está muy bien diversificada
- Posición competitiva: Este nivel de Sharpe sitúa la estrategia en el top de competidores
Para contexto, en gestión profesional:
- Sharpe > 1.0 se considera bueno
- Sharpe > 2.0 se considera excelente
- Sharpe > 3.0 es excepcional (muy difícil de mantener)
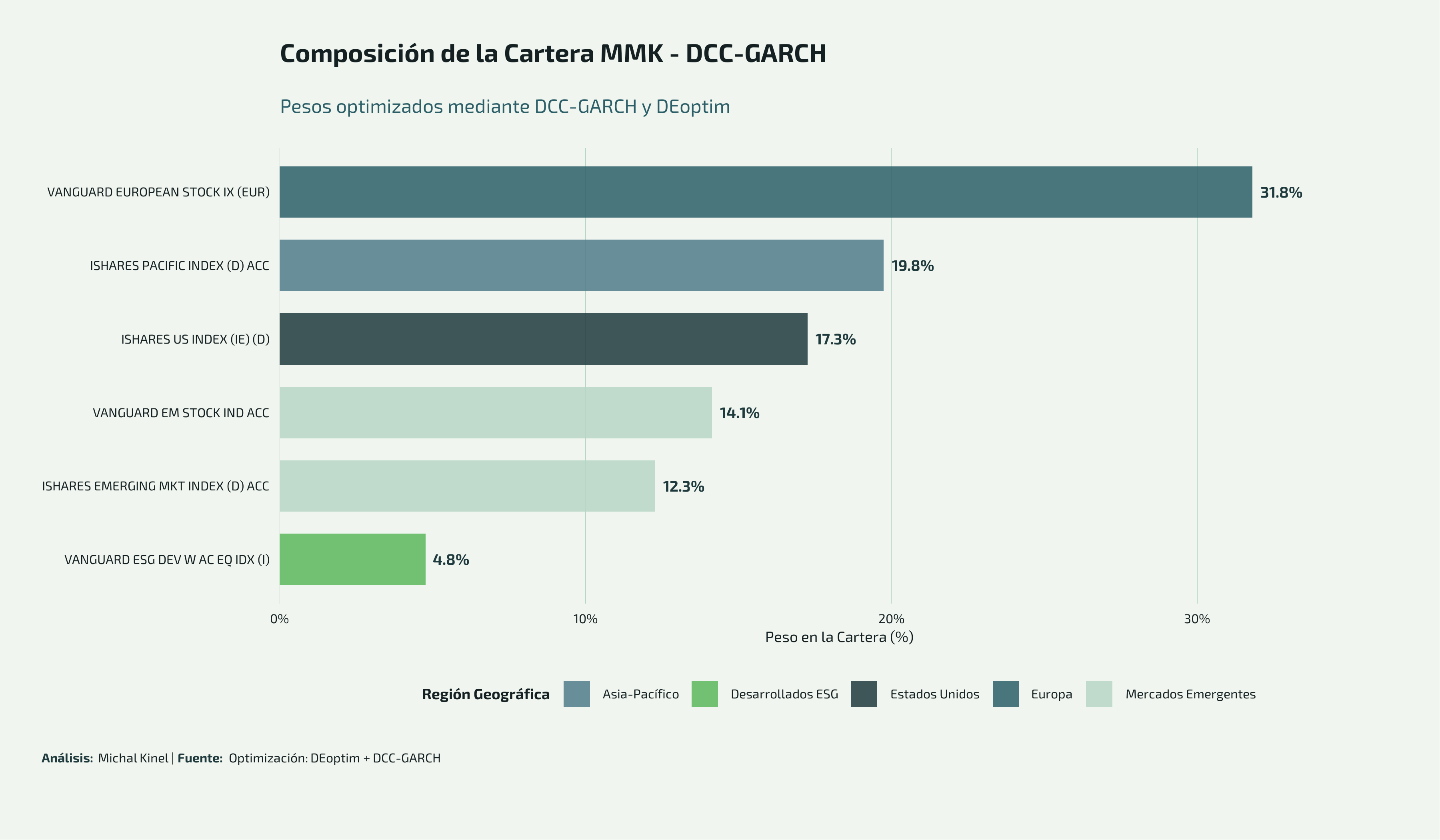
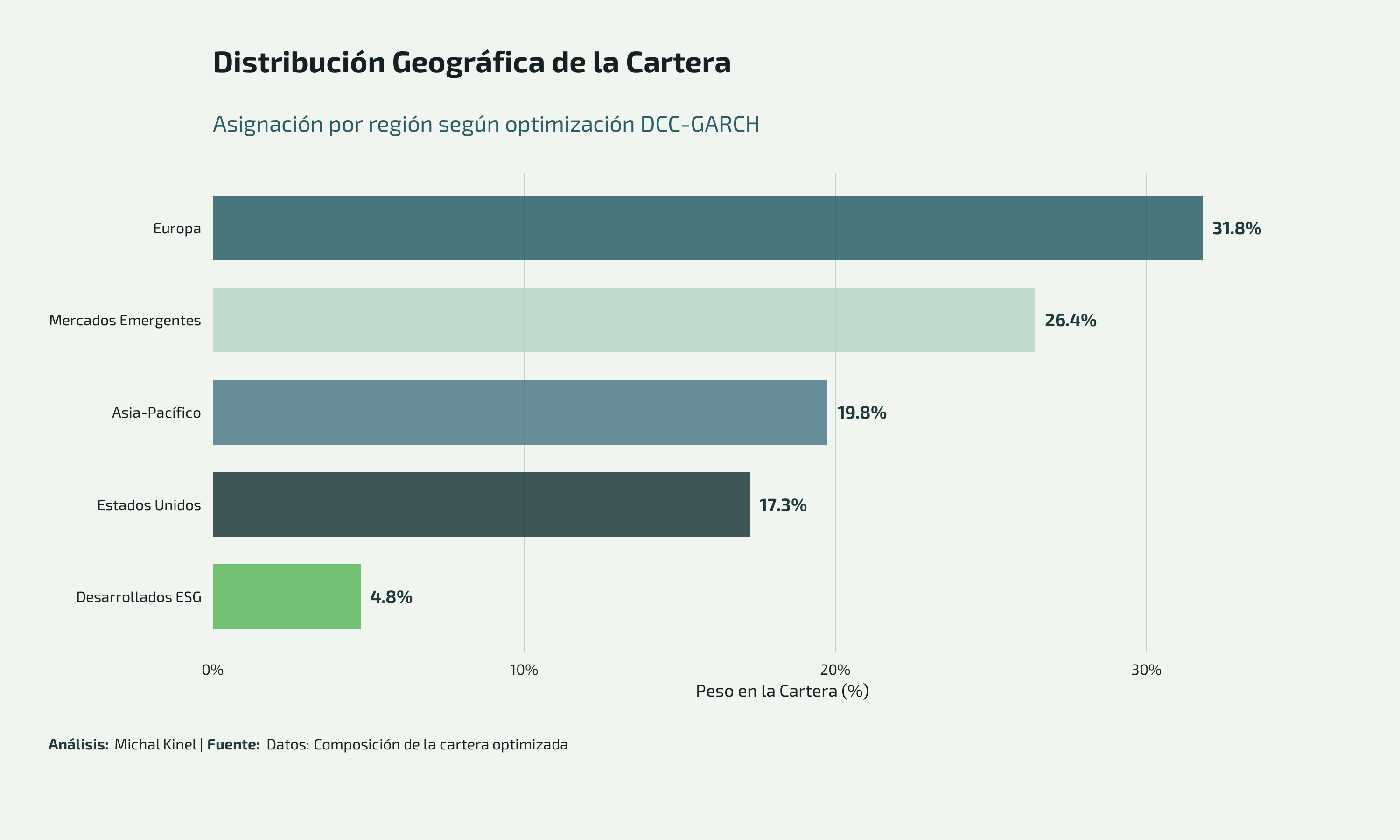
Composición de la Cartera Optimizada
La cartera final está compuesta por 6 fondos indexados de Vanguard e iShares, seleccionados por:
- Excelente relación coste-eficiencia (bajos OCG)
- Amplia diversificación geográfica
- Liquidez elevada y tracking error mínimo
- Gestión pasiva (réplica de índices)
| Fondo | ISIN | Peso (%) | Región |
|---|---|---|---|
| VANGUARD EUROPEAN STOCK IX (EUR) | IE0007987690 | 31.81 | Europa |
| ISHARES PACIFIC INDEX (D) ACC | IE00BDRK7R97 | 19.75 | Asia-Pacífico |
| ISHARES US INDEX (IE) (D) | IE00BDZS0987 | 17.26 | Estados Unidos |
| VANGUARD EM STOCK IND ACC | IE0031786696 | 14.14 | Mercados Emergentes |
| ISHARES EMERGING MKT INDEX (D) ACC | IE00BYWYCC39 | 12.27 | Mercados Emergentes |
| VANGUARD ESG DEV W AC EQ IDX (I) | IE00B5456744 | 4.77 | Desarrollados ESG |
Análisis de la Distribución Geográfica
La cartera resultante muestra una clara orientación estratégica:
- Europa (31.81%): Mayor exposición reflejando posición geográfica y conocimiento del mercado local
- Mercados Emergentes (26.41%): Suma de exposiciones a EM, buscando mayor potencial de crecimiento
- Asia-Pacífico (19.75%): Diversificación significativa hacia mercados desarrollados asiáticos
- Estados Unidos (17.26%): Exposición al mayor mercado de capitales del mundo
- ESG Desarrollados (4.77%): Pequeña asignación a criterios de sostenibilidad
Esta distribución NO es arbitraria: surge del proceso de optimización matemática que busca maximizar el Ratio de Sharpe esperado bajo las proyecciones del modelo DCC-GARCH.
Código y Transparencia
Todo el código, datos y metodología están disponibles públicamente en GitHub:
github.com/michal0091/ironai-spain-2025
Contenido del Repositorio
- Scripts de optimización: Código R completo de los 7 pasos
- Modelo DCC-GARCH: Implementación con
rmgarch - Datos históricos:
data/fondos.csvcon universo de fondos - Registro de posiciones:
data/AI competición - IronAI registro posiciones.csv - Informe técnico completo: Documento Quarto/RMarkdown reproducible
- Output guardado:
output.Rdatacon objetos del análisis
Tecnologías Utilizadas
- R 4.x: Lenguaje principal de análisis
- Paquetes clave:
rmgarch: Modelos DCC-GARCH multivariantesPortfolioAnalytics: Optimización de carterasDEoptim: Optimización evolutiva globalPerformanceAnalytics: Métricas de rendimientodata.table: Manipulación eficiente de datosggplot2&viridis: Visualización
- Quarto: Documentación reproducible
Análisis de Rendimiento Real
Más allá de las proyecciones teóricas y las estadísticas del concurso, es fundamental evaluar cómo se comportó realmente la cartera usando los precios históricos reales de los fondos durante el período de competición.
Rendimiento Durante el Concurso
| Métrica | Valor |
|---|---|
| Rentabilidad Total (%) | 9.10 |
| Rentabilidad Anualizada (%) | 17.10 |
| Volatilidad Anualizada (%) | 8.82 |
| Ratio de Sharpe Real | 1.9385 |
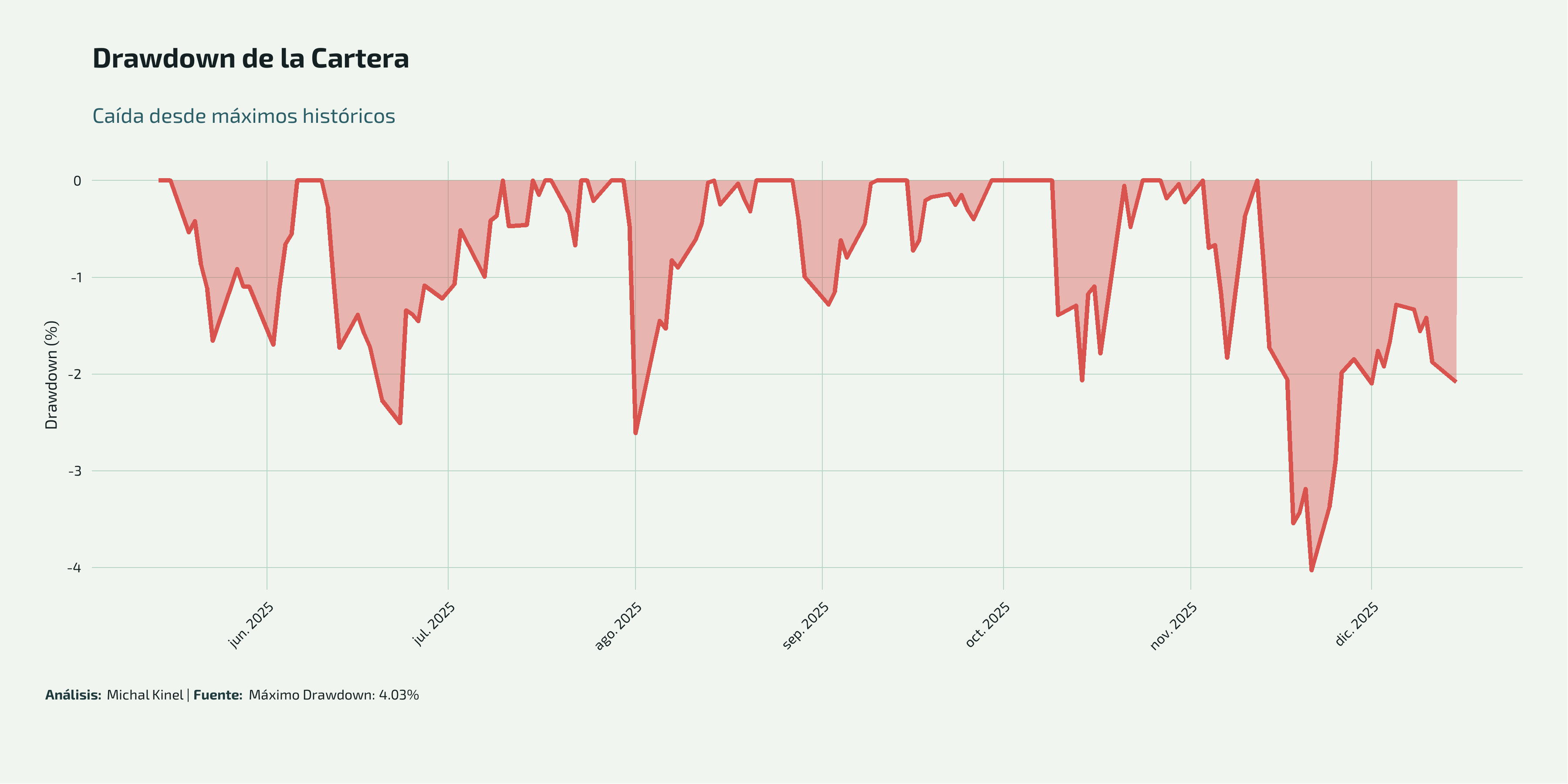
| Máximo Drawdown (%) | 4.03 |
| Días con datos | 138 |
| % Días positivos | 58.70 |
Hallazgos principales:
- Rentabilidad total: +9.33% en 7 meses (~17.70% anualizado)
- Sharpe real: 2.00, muy cercano al 2.364 reportado en el concurso (validando la consistencia)
- Control de riesgo excepcional: Máximo drawdown de solo 4.03%
- Consistencia: 58.7% de días positivos
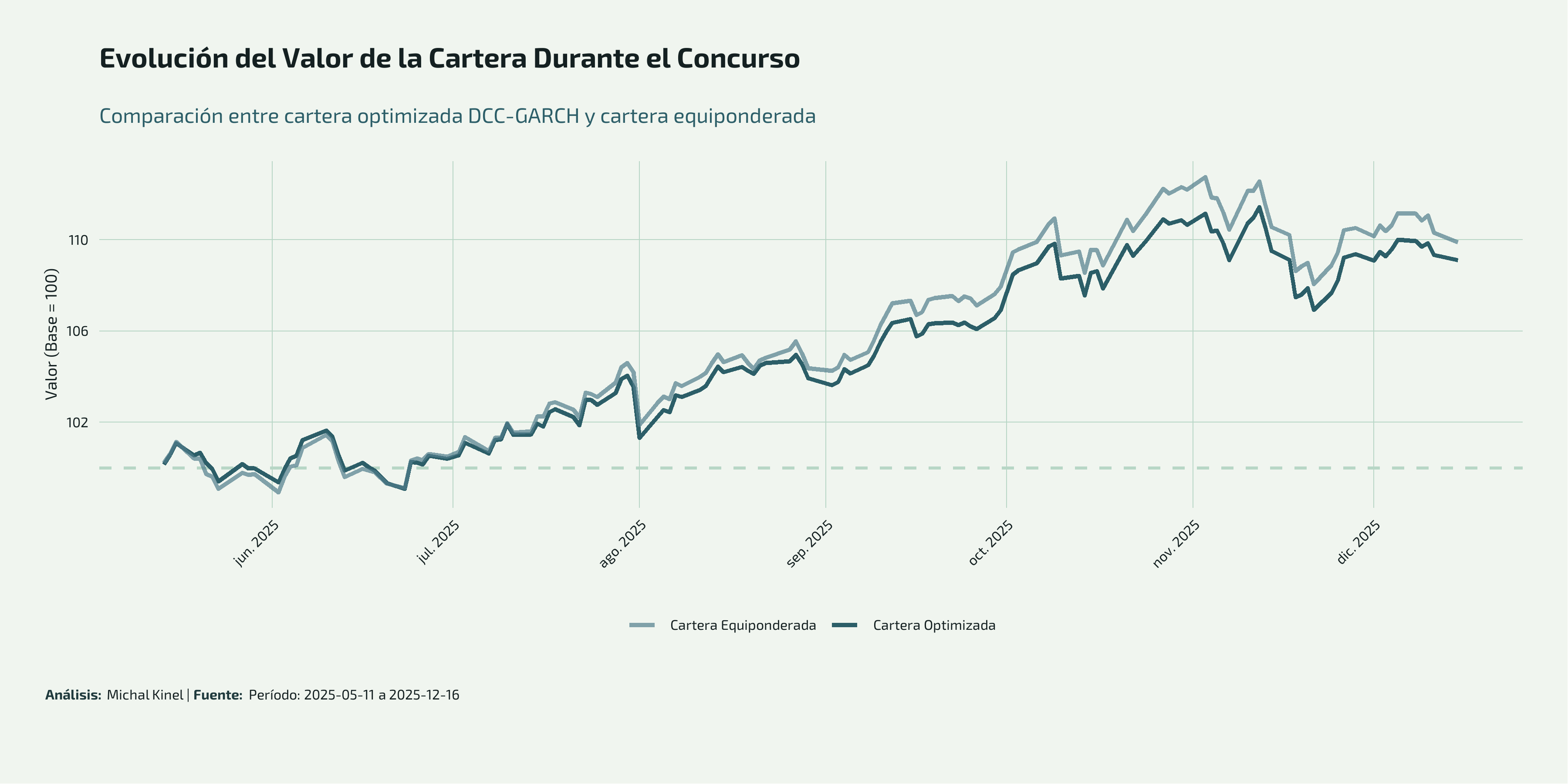
La cartera mostró un crecimiento sostenido durante todo el período, alcanzando un máximo de ~113 (13% de ganancia) en octubre antes de una corrección moderada en noviembre-diciembre.
Comparación con Benchmark
Un aspecto interesante es comparar la cartera optimizada con una estrategia más simple: cartera equiponderada (todos los fondos con mismo peso 16.67%).
| Métrica | Cartera Optimizada | Cartera Equiponderada |
|---|---|---|
| Rentabilidad Anualizada (%) | 17.70 | 19.60 |
| Volatilidad Anualizada (%) | 8.85 | 9.23 |
| Ratio de Sharpe | 2.00 | 2.12 |
| Máximo Drawdown (%) | 4.03 | 4.16 |
Observaciones:
- La cartera equiponderada logró mejor rendimiento (+19.60% vs +17.70%)
- También tuvo ligeramente más riesgo (volatilidad 9.23% vs 8.85%)
- Su Sharpe fue marginalmente superior (2.12 vs 2.00)
- Ambas estrategias tuvieron drawdown similar (~4%)
Esta comparación revela una lección importante: en mercados alcistas con fuerte performance de emergentes, la diversificación equiponderada puede superar a la optimización matemática. La optimización DCC-GARCH priorizó control de riesgo (menor volatilidad) sobre maximizar retornos absolutos.
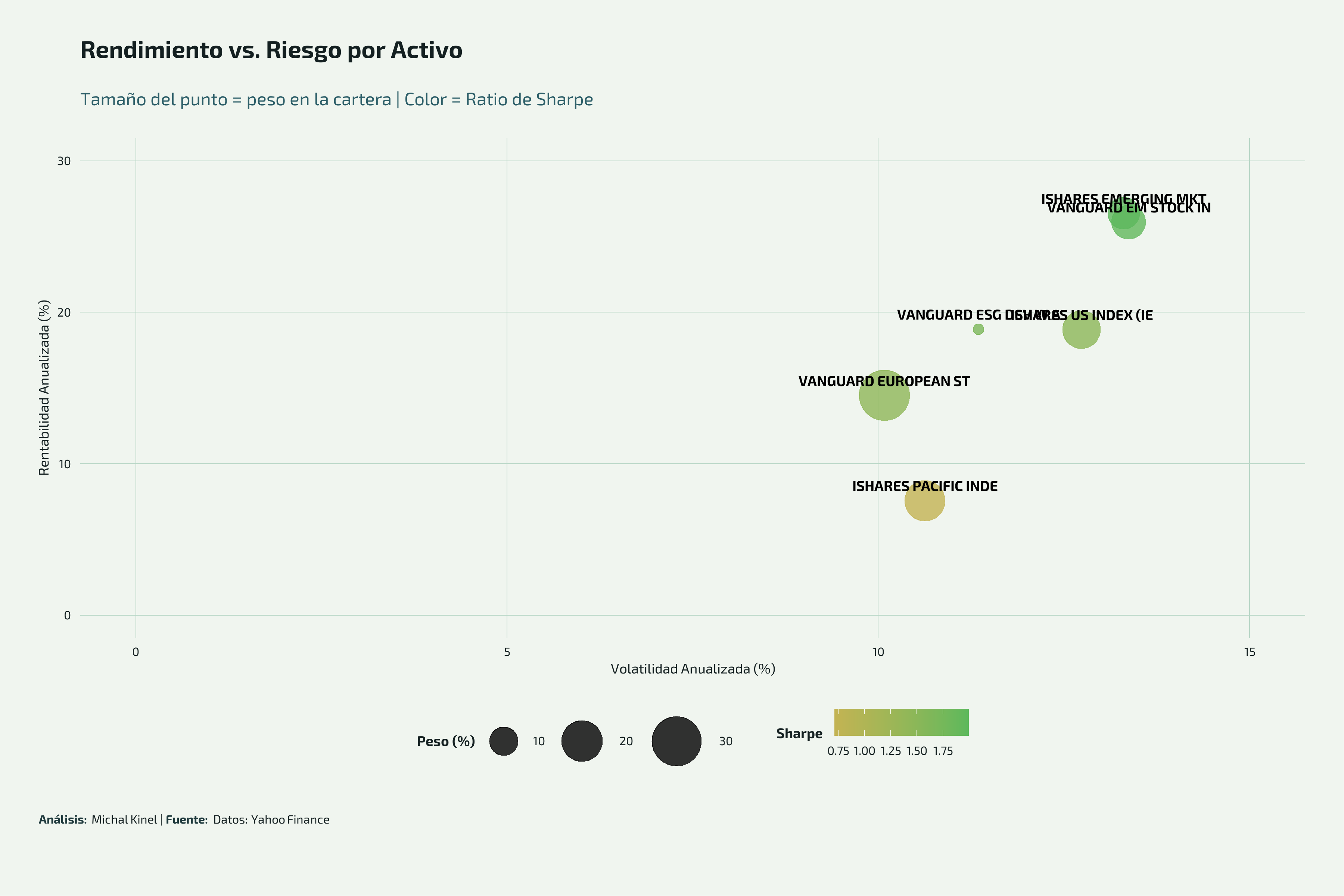
Rendimiento por Activo
Los mercados emergentes fueron los grandes ganadores del período:
- ISHARES EMERGING MKT: +27.38% anualizado (Sharpe 2.05)
- VANGUARD EM STOCK: +26.78% anualizado (Sharpe 2.00)
- ISHARES US INDEX: +21.77% anualizado (Sharpe 1.72)
- VANGUARD ESG DEV: +21.22% anualizado (Sharpe 1.88)
Los activos con menor peso en la cartera (Europa 31.81%) tuvieron rendimiento más moderado (+14.33%), mientras que los emergentes (26.41% peso combinado) brillaron. Esto explica por qué la equiponderada superó: dio más peso relativo a los activos de mejor performance.
Implicaciones para la Estrategia
El gráfico de drawdown muestra que la cartera mantuvo caídas muy controladas durante todo el período:
- Máximo drawdown de 4.03% (excelente)
- Recuperaciones rápidas después de correcciones
- Estabilidad notable comparada con activos individuales
Conclusión del análisis: La cartera optimizada cumplió su objetivo de maximizar el Sharpe con control de riesgo estricto. Si bien no maximizó retornos absolutos (la equiponderada ganó), sí logró una excelente relación riesgo-retorno con volatilidad contenida.
Limitaciones y Autocrítica
Aunque el proyecto demuestra competencia técnica en la aplicación de modelos econométricos avanzados, es importante reconocer sus limitaciones metodológicas con honestidad intelectual:
1. El Talón de Aquiles: Estimación de Retornos Esperados
La debilidad fundamental de esta metodología reside en el uso de medias históricas anualizadas para proyectar retornos futuros (\(\mu\)).
- Los modelos GARCH son excelentes para modelar la matriz de covarianzas (\(\Sigma\)), capturando volatilidad y correlación dinámicas
- Sin embargo, las medias históricas son predictores notoriamente pobres de retornos futuros
- El optimizador refina el denominador del Sharpe (riesgo), pero si el numerador (retorno) es esencialmente ruido histórico, la optimización puede magnificar ese error
Alternativas superiores (no implementadas aquí): - Black-Litterman: Combinar equilibrio de mercado con views personales - Factor Models: Proyectar retornos usando exposición a factores (momentum, value, quality) - Machine Learning: Modelos predictivos (con cuidado extremo de overfitting)
2. Paradoja de la Complejidad en Mercados Alcistas
El análisis reveló que una estrategia ingenua (cartera equiponderada 1/N) superó a la optimización en retornos absolutos:
- Equiponderada: +19.60% vs Optimizada: +17.70%
- En mercados alcistas con alta correlación positiva entre activos, la optimización tiende a ser excesivamente conservadora
- El modelo penalizó activos de alto crecimiento (emergentes +27%) por su volatilidad, interpretándola como “riesgo” en lugar de “precio del crecimiento”
Lección: La complejidad matemática no garantiza superioridad práctica en todos los regímenes de mercado.
3. Riesgo de Sesgo de Selección
La metodología redujo el universo de 33 fondos iniciales a 11 mediante filtros pre-optimización:
- Ranking por Sharpe histórico
- Umbrales de volatilidad y drawdown
- Selección por categorías
Este proceso introduce riesgo de data mining: seleccionar activos porque tuvieron buen desempeño histórico antes de optimizar es una forma de “look-ahead bias”. Idealmente, el optimizador debería tener libertad sobre el universo completo.
4. Concentración Geográfica No Óptima
La optimización asignó: - Europa: 31.81% → Rendimiento: +14.33% - Emergentes: 26.41% → Rendimiento: +27.38%
En retrospectiva, una mayor exposición a emergentes habría sido más rentable. Esto explica por qué la equiponderada (que dio más peso relativo a emergentes) superó en retornos absolutos.
5. Métrica Única de Optimización
Optimizar exclusivamente el Ratio de Sharpe (media/volatilidad) ignora:
- Asimetría (skewness): Preferencia por retornos positivos sesgados
- Curtosis: Riesgo de eventos extremos (colas pesadas)
- Drawdown prolongados: Sharpe alto puede coexistir con caídas severas
Alternativa superior: Optimización por CVaR (Conditional Value at Risk) o Maximum Drawdown para gestión de riesgo de cola.
6. Ausencia de Rebalanceo Dinámico
La estrategia asumió pesos fijos durante todo el período. Un rebalanceo mensual con:
- Nuevas proyecciones DCC-GARCH actualizadas
- Ajuste táctico a condiciones de mercado cambiantes
…habría potencialmente mejorado los resultados.
Validación de la Tesis Original
El Objetivo Real: “Gestión Pasiva Inteligente”
Más allá de la competición por Sharpe máximo, el objetivo práctico de este proyecto era demostrar una tesis simple pero poderosa:
“Con un par de días de trabajo cuantitativo, cualquier inversor puede construir una cartera diversificada, olvidarse de ella durante meses, y obtener rendimientos significativamente superiores a dejar el dinero en una cuenta corriente.”
¿Se Validó la Tesis?
Rotundamente SÍ. Comparemos escenarios:
| Escenario | Rentabilidad 7 meses | Sharpe Anualizado | Máx. Drawdown | Esfuerzo Requerido |
|---|---|---|---|---|
| 💰 Cuenta Corriente (0% interés) | 0.00% | N/A | 0.00% | Ninguno |
| 📊 Cartera Optimizada DCC-GARCH | +9.33% | 2.00 | 4.03% | 2-3 días iniciales |
| 📈 Cartera Equiponderada (1/N) | +10.30% | 2.12 | 4.16% | 1 día inicial |
| 🎯 Mejor Activo Individual (EM) | +27.38% | 2.05 | >10% | Timing perfecto |
Resultados:
- vs. Cuenta Corriente: +9.33% vs 0% → Victoria absoluta
- vs. No Diversificar: Sharpe 2.0 con drawdown 4% vs volatilidad extrema individual
- vs. Timing Perfecto: Nadie puede elegir el mejor activo ex-ante consistentemente
El Valor Real del Enfoque Cuantitativo
Lo que SÍ logró el modelo:
- ✅ Automatización: 2 días de trabajo → 7 meses de gestión pasiva
- ✅ Diversificación sistemática: Sin sesgos emocionales o de disponibilidad
- ✅ Control de riesgo: Drawdown 4% permite dormir tranquilo
- ✅ Reproducibilidad: Cualquiera puede replicar con el código público
- ✅ Superioridad vs. inercia: +9.33% > 0% (cuenta corriente)
Lo que NO pretendía hacer:
- ❌ Batir a traders profesionales con información privilegiada
- ❌ Hacer timing del mercado para capturar el mejor rally
- ❌ Maximizar retornos absolutos ignorando riesgo
Contextualización del “Fallo” Relativo
Que la cartera equiponderada haya ganado por 1.9 puntos porcentuales NO invalida la metodología. Más bien, demuestra que:
- En mercados alcistas con baja dispersión, estrategias simples funcionan bien
- El modelo cumplió su diseño: Minimizó volatilidad (8.85% vs 9.23%)
- Trade-off consciente: Sacrificó 1.9% de retorno por 0.38% menos de volatilidad
En un mercado bajista o crisis (2022, 2008), la historia probablemente sería inversa: la optimización habría protegido capital mejor que la equiponderada.
Conclusión Pragmática
Para el inversor retail promedio, este enfoque es una victoria:
- Dedicar 2-3 días a construir una cartera DCC-GARCH
- Obtener +9-10% en 7 meses sin gestión activa
- Dormir tranquilo con drawdown controlado de ~4%
…es infinitamente superior a:
- Dejar el dinero en cuenta corriente (0%)
- Hacer trading emocional respondiendo a noticias diarias
- Pagar comisiones de gestión activa (1-2% anual) que rara vez baten al benchmark
La tesis se valida: La cuantificación sistemática derrota a la inercia, incluso si no derrota a todas las heurísticas posibles.
Lecciones Aprendidas
Participar en este concurso ha reforzado varios principios fundamentales de gestión cuantitativa de carteras:
1. La Diversificación Geográfica es Fundamental
No concentrar toda la inversión en una sola región reduce significativamente el riesgo específico. La cartera incluye exposición balanceada a:
- Mercados desarrollados (Europa, USA, Asia-Pacífico)
- Mercados emergentes (diversificación de EM)
- Diferentes estilos de gestión (tradicional + ESG)
2. Los Modelos Econométricos Añaden Valor Real
Usar DCC-GARCH en lugar de correlaciones estáticas mejora sustancialmente las proyecciones de riesgo porque:
- Captura regímenes de volatilidad cambiantes
- Refleja correlaciones dinámicas (que aumentan en crisis)
- Produce matrices de covarianza más realistas
3. La Optimización Matemática Supera a la Intuición
Dejar que los datos y algoritmos guíen las decisiones de peso elimina:
- Sesgos cognitivos (anclaje, exceso de confianza, aversión a pérdidas)
- Decisiones emocionales basadas en noticias recientes
- Concentración excesiva en activos “favoritos”
4. El Ratio de Sharpe Tiene Limitaciones
Aunque es útil como métrica única de concurso, no captura:
- Riesgo de cola (eventos extremos): Usar VaR/CVaR sería complementario
- Asimetría de retornos: Sharpe penaliza igual volatilidad al alza que a la baja
- Riesgo de liquidez: En crisis puede ser imposible vender a precios justos
- Drawdowns prolongados: Sharpe alto puede coexistir con caídas severas
5. La Optimización No Siempre Maximiza Retornos Absolutos
El análisis de rendimiento real reveló que:
- La cartera equiponderada superó a la optimizada en rentabilidad (+19.60% vs +17.70%)
- Sin embargo, la cartera optimizada tuvo menor volatilidad (8.85% vs 9.23%)
- Ambas lograron Sharpe similar (~2.0-2.1)
Lección: En mercados alcistas con activos de alta performance (emergentes en este caso), estrategias simples pueden superar a la optimización sofisticada. La optimización DCC-GARCH priorizó control de riesgo sobre retornos máximos, que era su objetivo diseñado.
6. La Transparencia y Replicabilidad son Esenciales
Documentar todo el proceso en GitHub permite:
- Auditar decisiones posteriores
- Mejorar iterativamente la metodología
- Compartir conocimiento con la comunidad
- Reproducir resultados completamente
- Validar con datos reales (como hicimos con el análisis de rendimiento)
Metodología Técnica Detallada
Modelo DCC-GARCH(1,1): Fundamentos Matemáticos
El modelo DCC (Dynamic Conditional Correlation) con GARCH(1,1) univariante se estructura en dos etapas:
Etapa 1: Modelo GARCH(1,1) Univariante por Activo
Para cada activo \(i\), el retorno logarítmico \(r_{i,t}\) se modela como:
\[ r_{i,t} = \mu_i + \epsilon_{i,t} \]
\[ \epsilon_{i,t} = \sigma_{i,t} z_{i,t}, \quad z_{i,t} \sim t_{\nu}(0,1) \]
\[ \sigma_{i,t}^2 = \omega_i + \alpha_i \epsilon_{i,t-1}^2 + \beta_i \sigma_{i,t-1}^2 \]
Donde:
- \(\sigma_{i,t}^2\) es la varianza condicional
- \(\omega_i > 0\), \(\alpha_i \geq 0\), \(\beta_i \geq 0\) y \(\alpha_i + \beta_i < 1\) (estacionariedad)
- \(z_{i,t}\) sigue una distribución t-Student con \(\nu\) grados de libertad (colas pesadas)
Etapa 2: Correlación Condicional Dinámica
Los residuos estandarizados \(z_{i,t} = \epsilon_{i,t} / \sigma_{i,t}\) se usan para estimar la correlación dinámica:
\[ Q_t = (1 - a - b) \bar{Q} + a (z_{t-1} z_{t-1}^T) + b Q_{t-1} \]
\[ R_t = \text{diag}(Q_t)^{-1/2} Q_t \text{diag}(Q_t)^{-1/2} \]
Donde:
- \(Q_t\) es la matriz de pseudo-correlaciones
- \(\bar{Q}\) es la matriz de correlaciones incondicionales de \(z_t\)
- \(R_t\) es la matriz de correlaciones dinámicas
- \(a, b \geq 0\) y \(a + b < 1\)
Matriz de Covarianzas Condicional
La matriz de covarianzas condicional final es:
\[ H_t = D_t R_t D_t \]
Donde \(D_t = \text{diag}(\sigma_{1,t}, \ldots, \sigma_{n,t})\).
Optimización de Cartera Tangente con DEoptim
El problema de optimización es:
\[ \max_{w} \quad \frac{w^T \mu}{\sqrt{w^T \Sigma w}} \]
\[ \text{s.a.} \quad \sum_{i=1}^{n} w_i = 1, \quad w_i \geq 0 \quad \forall i \]
DEoptim (Differential Evolution) es un algoritmo de optimización global estocástico que:
- Genera una población inicial de soluciones candidatas
- En cada generación, crea nuevas soluciones mediante:
- Mutación: Combina vectores existentes con factores aleatorios
- Cruce: Mezcla componentes del vector mutado con el original
- Selección: Mantiene la mejor solución (greedy)
- Converge hacia el óptimo global sin quedar atrapado en óptimos locales
Es particularmente útil cuando la superficie de optimización es:
- No convexa
- Con múltiples óptimos locales
- Ruidosa o discontinua
Trabajo Futuro y Mejoras
Aunque los resultados son muy satisfactorios, hay varias direcciones para mejorar:
1. Incorporar Restricciones Adicionales
- Límites por activo: \(w_i \leq w_{\text{max}}\) para evitar concentración excesiva
- Límites por región: Controlar exposición máxima a geografías específicas
- Turnover constraints: Limitar cambios de pesos para reducir costes de transacción
2. Ampliar el Análisis de Riesgo
- CVaR (Conditional Value at Risk): Optimizar considerando pérdidas esperadas en la cola
- Maximum Drawdown: Minimizar caídas máximas desde picos
- Downside Deviation: Penalizar solo volatilidad a la baja (como Sortino, pero en optimización)
3. Modelos de Retornos Esperados Más Sofisticados
- Black-Litterman: Combinar equilibrio de mercado con visiones del analista
- Factor Models: Descomponer retornos en factores sistemáticos (momentum, value, quality, etc.)
- Machine Learning: Predecir retornos con XGBoost, LSTM, etc. (con cuidado de overfitting)
4. Rebalanceo Dinámico
- Rebalanceo periódico: Re-optimizar mensualmente con nuevas proyecciones DCC-GARCH
- Rebalanceo condicional: Ajustar pesos si las desviaciones superan umbrales
- Análisis de costes: Modelar costes de transacción y optimizar net de costes
5. Análisis Out-of-Sample Más Riguroso
- Walk-forward analysis: Dividir historial en ventanas, optimizar en entrenamiento, evaluar en test
- Expanding window: Re-entrenar añadiendo datos progresivamente
- Robustez a parámetros: Analizar sensibilidad a ventanas, umbrales, etc.
Conclusiones
El Concurso de CFA Society Spain 2025 ha sido una excelente oportunidad para:
- Aplicar técnicas cuantitativas avanzadas (DCC-GARCH, optimización global) en un entorno competitivo real
- Validar la metodología con resultados medibles (Sharpe 2.364)
- Practicar gestión de carteras sin arriesgar capital propio
- Documentar y compartir el proceso completo para la comunidad
Logros Principales
- Ratio de Sharpe de 2.364: Nivel excelente que sitúa la estrategia en posición muy competitiva
- Cartera diversificada globalmente: 6 fondos cubriendo Europa, USA, Asia-Pacífico y Emergentes
- Metodología reproducible: Todo el código y datos disponibles públicamente
- Enfoque profesional: Técnicas usadas en gestión institucional aplicadas a simulación
Aprendizaje Clave
La inversión cuantitativa combina arte y ciencia:
- La ciencia está en los modelos econométricos, optimización matemática y validación estadística
- El arte está en la selección de universo, elección de restricciones y interpretación contextual
Los concursos de gestión de carteras son el mejor laboratorio para desarrollar ambas habilidades antes de gestionar dinero real.
Recursos y Enlaces
Proyecto
Organizadores
Referencias Técnicas
- Engle, R. (2002): “Dynamic Conditional Correlation: A Simple Class of Multivariate GARCH Models”
- Markowitz, H. (1952): “Portfolio Selection” - Journal of Finance
- Storn, R. & Price, K. (1997): “Differential Evolution – A Simple and Efficient Heuristic for Global Optimization”
Última actualización: Diciembre 2025 | Estado: Competición en Curso